DSP Notları : Filtreler – 1 – Finite Impulse Response

Bir önceki yazı dizisinde filtreler konusuna bir giriş yapmış ve seriyi temel bir uygulama ile sonlandırmıştık. Bu yazı serisinde filtreleme konusuna biraz daha derinlemesine girmeyi hedefliyorum. Önceki serilerde teoriden sıkılan okuyucular son yazıdaki uygulamayı görünce bir hayli sevinmiş ve güzel geri dönüşler yapmışlardı. Sanırım teori ve pratiğin bu şekilde birleştiğini görmek okuyuculara matematiğin aslında bu kadar soyut olmadığını ve mühendisliği dolaylı olarak değil doğrudan etkilediğini gösterdi. Artık soyut ve oldukça korkutucu gözüken matematiğin gerçekte böyle olmadığını anladığımıza göre filtreleme konusunu daha deri bir şekilde inceleyebiliriz. Başlamadan önce bir konuyu dile getirmem gerekiyor. Bu yazı serilerini okurken, “Buna ihtiyacımız olmayacak çünkü Matlab bu işleri bizim için yapıyor.” gibi bir ifadeyi kullanmakta oldukça haklı olabilirsiniz fakat bizim amacımız bu işin mantığını ve temelini anlamak hatta daha da öte bir gereksinim olan ve mühendislik yapmak için ihtiyaç duyduğumuz muhakeme yeteneğini geliştirmek, buradaki birincil amacımızdır. Ek olarak filtreleme konusunda karşılaşacağımız zorlu problemlerde, iyi bir alt yapının faydasını göreceğinizi garanti edebilirim. Eğer hazırsanız zihnimizi çok yumuşak bir filtreden geçirelim.

Öncelikle okumadıysanız bir önceki seriyi mutlaka gözden geçirin.

• İstenmeyene Göğüs Gerenler : Filtreler – 1
• İstenmeyene Göğüs Gerenler : Filtreler – 2 – Bilinear Z Transform (Tustin Transform)
• İstenmeyene Göğüs Gerenler : Filtreler – 3 – Sinyal İşleme Uygulaması

Filtreleme ile çalışırken sıkça karşılaşacağınız FIR ve IIR terimleri aslında birer teknik olarak düşünülebilir. Daha doğrusu bunlar “Impulse Response” çeşitleri olarak adlandırılır. Sonlu ve sonsuz olmak üzere iki çeşidi vardır.

• FIR (Finite Impulse Response)
• IIR (Infinite Impulse Response)

Her yapını kendine göre özellikleri, avantajları ve dezavantajları var. Aslında burada kullanacağınız yere göre seçim yapmanız gerekebilir. Peki öncelikle bir şeyi hatırlayalım. Filtre dediğimiz şey matematiksel olarak nedir ? Ayrık zaman için bir katsayı dizisinden ibaret değil midir ? O halde notasyona uygun olması adına bu katsayı dizisine $h[n]$ diyelim. Her zaman olduğu gibi giriş işaretine $x[n]$ filtrelenmiş çıkış işaretine ise $y[n]$ diyelim. O halde filtrelenmiş çıkış işaretini şu şekilde ifade ederiz.

$$y[n] = x[n] \ast h[n]$$

Bu işleme “Discrete Convolution” yani “Ayrık Konvolüsyon” denir. Zaman ekseninde çarpma işlemi neyse, frekans ekseninde çarpma işleminede konvolüsyon denir. Soru şu; katsayıları nasıl elde ederiz ?

FIR (Finite Impulse Response)

FIR geri beslemesiz bir filtre modelidir. Burada notasyonların karışmaması adına $h[n] = b[n]$ olarak tanımlama yapalım. Bu ifadenin toplam sembolü ile açılımı şu şekildedir.

$$y[n] = \sum_{m=0}^{N}b[n – m]x[m]$$

Bu ifadeye bakacak olursak elde edeceğimiz denklemin sol tarafı $y[n]$, sağ tarafı ise $b[n] x[n]$ içeren ifadelerden oluşacak. Bu yapı rekürsif değildir.

$$y[n] = b[n] x[0] + b[n – 1]x[1] + b[n – 2]x[2] + … + b[n – N]x[N]$$

O halde bir FIR filtrenin modeli aşağıdaki gibi olur.

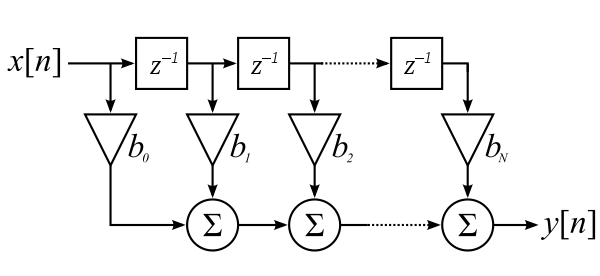
Tasarım aşamasında bir çok metot vardır. Bunlardan en yaygın olanı “Window Design Method” yani “Pencere Tasarım Metot” olarak bilinir. Pencere işlemleri kendi içinde ayrılır. Bu yazıda “Rectengular Window” olarak adlandırılan pencere yapısını inceleyelim. Bu pencere yapısını özellikle “Low Pass” yani alçak geçiren filtre için kullandığını görürüz. Öncelikle bir “Rectengular Window” şu şekilde tanımlanır.

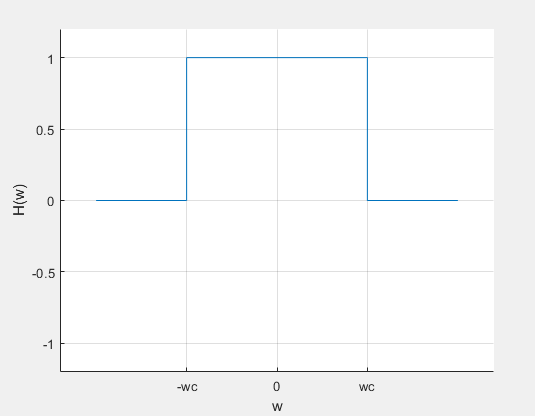
Yukarıda görüldüğü üzere bu alçak geçiren bir filtre modeli. Bunun sebebi ise $H(\omega)$ fonksiyonu $0 \leq \omega \leq \omega_{c}$ aralığında 1, diğer durumlarda ise 0 değerlerini almasından kaynaklıdır. Burada ideal bir filtre için bu fonksiyonu Ters Fourier Dönüşümü(IFT – Inverse Fourier Transform) yaparak $h_{d}(n)$ fonksiyonunu elde edebiliriz. Dikkat ettiyseniz bu fonksiyonu $h_{d}(n)$ olarak adlandırdım $h_{d}(n)$ olarak değil. Bunun sebebini birazdan göreceğiz. O halde Ters Fourier Dönüşümü yaparak frekans ekseninden çıkalım.

Ters Fourier Dönüşümü şu şekilde tanımlanır;

$$\mathcal{F}^{-1}\{H(\omega)\}=\frac{1}{2\pi} \int_{-\infty}^{+\infty}H(\omega)e^{j\omega n}d\omega$$

$$h_{d} [n]=\frac{1}{2\pi} \int_{-\infty}^{+\infty}H_{d}(\omega)e^{j\omega n}d\omega$$

Elimizdeki fonksiyon parçalı halde çözülürse 0 olan kısımlar integrali sıfır yapar ve sonucu eklemez o halde sınırları $-\omega_{c}$ ile $\omega_{c}$ arasında sınırlayabiliriz. Anlaşılır olması adına integral çözüm işlemlerini aşağıda adım adım gerçekleştirelim.

$$h_{d} [n]=\frac{1}{2\pi} \int_{-\omega}^{\omega}1(\omega)e^{j\omega n}d\omega$$

$$= \left.\frac{1}{2\pi}\left (\frac{1}{jn}e^{j\omega n}\right)\right|_{-\omega_{c}}^{+\omega_{c}}$$

$$= \frac{1}{2\pi jn}\left (e^{j\omega_{c} n} – e^{-j\omega_{c} n}\right)$$

$$= \frac{1}{2\pi}\left (\frac{e^{j\omega_{c} n} – e^{-j\omega_{c} n}}{jn}\right)$$

$$sin(\omega_{c}n) = \frac{e^{j\omega_{c} n} – e^{-j\omega_{c} n}}{jn}$$

olduğundan ötürü sonuç, aşağıdaki gibi olur.

$$h_{d}[n] = \frac{sin(\omega_{c}n)}{\pi n}$$

Bulduğumuz fonksiyonu ayrık olarak kullanmak için $0, 1, 2 … N$ şeklinde indis vererek $N$. dereceden bir dizi elde edebiliriz. Dikkat ederseniz ilk katsayı olan $n = 0$ noktasında bir  $\frac{0}{0}$ belirsizliği var. Limit kullanarak 0 noktasına yaklaşmaya çalıştığımızda bu belirsizliği L’Hôpital ile çözebiliriz.

$$\lim_{x\rightarrow 0}{\frac{\sin(\omega_{c}n)}{\pi n}}$$

$$ = \lim_{x\rightarrow 0}{\frac{\cos(\omega_{c}n){\omega_{c}}}{\pi}}$$

$$ = \frac{\cos(\omega_{c}0){\omega_{c}}}{\pi}$$

$$ = \frac{\cos(0){\omega_{c}}}{\pi}$$

$$ = \frac{\omega_{c}}{\pi}$$ 

olduğu görülmektedir. O halde $h_{d}[n]$ fonksiyonun tanımını artık verebiliriz.

$$h_{d}[n] = \begin{cases} \frac{sin(\omega_{c}n)}{\pi n} & n\neq 0 \\ \frac{\omega_{c}}{\pi} & n = 0 \\ \end{cases}$$

Bulduğumuz fonksiyon sonsuz girdi alabilen bir dizi (Infinite) yapıdadır. Bunun fonksiyonun(ayrık dizi) sonlu olabilmesi için sonlu bir pencere ile çarpılması gerekir. Biz Rectengular penceresini kullandığımız için bu sonsuz diziyi sonlu dizi olan Rectengular penceresi ile çarparsak sonlu(Finite) bir dizi elde ederiz. Bu yüzden gerçek $h[n]$ dizisi şu şekilde tanımlanır.

$$ h[n] = h_{d}[n]w[n]$$

$$w[n] = \begin{cases} 1 & -\omega_{c} \leq \omega \leq \omega_{c} \\ 0 & otherwise \end{cases}$$

Pencere fonksiyonu ilgili $-\omega_{c} \leq \omega \leq \omega_{c}$ aralığında 1 diğer durumlarda sıfır olduğundan $h[n] = h_{d}[n]$‘e eşit olur. Her pencere fonksiyonu’nun $w[n]$ dizisi farklı olduğundan bu değerler diğer pencere yapıları için geçerli değildir. Ayrıca belirtmek gerekir ki bulduğumuz $h[n]$ fonksiyonuna $sinc$ fonksiyonu adı verildiğini unutmayın. Bir çok döküman da bu tanımı görebilirsiniz. Elde ettiğimiz fonksiyonun bu hali ile kullanılması doğru değil. Bildiğiniz üzere sinc fonksiyonu negatif eksene de yayılıyor. Bunun önüne geçmek adına merkezden yarısı kadar kaydırma (shift) yapılmalı. Merkezi tespit etmek için eleman sayısını ikiye bölmek yeterlidir. Eleman sayısı $N$ olmak üzere $N = order$ ve $M$ ise tam merkez olduğundan ötürü $M = N / 2$ olduğunu ve tasarlanan filtrenin $N + 1$ adet katsayıya sahip olacağını görebiliriz. O halde bir “Rectengular Window Low Pass FIR” Filtre aşağıdaki gibi tanımlanır.

$$h[n] = \begin{cases} \frac{sin(\omega_{c}(n – M))}{\pi (n – M)} & n\neq M \\ \frac{\omega_{c}}{\pi} & n = M \\ \end{cases}$$

$$\omega_{c} = \frac{2\pi f_{c}}{f_{s}}$$

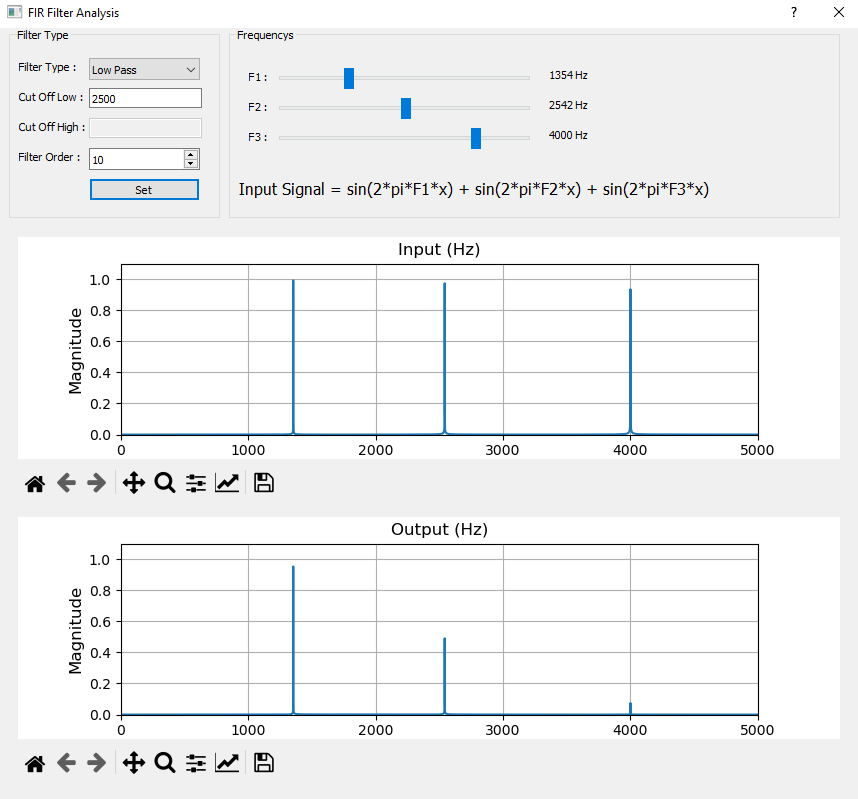
Bütün matematiksel alt yapıyı çıkardığımıza göre bir örnek tasarım gerçekleştirelim.Örnek işlemi için yine Python kullanarak FFT ve görselleştirme işlemlerini kolayca yapabiliriz. Aşağıdaki örnekte bir Python programında QT kullanarak yaptığım giriş ve çıkış spektrumlarını gösteren programa ulaşabilirsiniz. Program içerisinde 4 çeşit filtre bulunuyor. Diğer filtrelerin anlatımlarını daha sonra yapmayı düşünüyorum Kullanılan yapı genel olarak aynı. Aşağıdaki özelliklere sahip bir filtreyi tasarlayalım.

• $Order = 10$
• $f_{s} = 20  kHz$
• $f_{c} = 2.5 kHz$

İşlemleri yaptığınız zaman bulduğumuz katsayılar şöyle olacaktır;

$$h[n] = \{-0.045016, 0.0, 0.075026, 0.159155, 0.225079, $$

$$0.25,$$

$$0.225079, 0.159155, 0.075026, 0.0, -0.045016 \}$$

Filtrenin çıktısı aşağıdaki gibi olacaktır.

Her şey yolunda gözüküyor. Python programını ve QT arayüz tasarımını Github hesabımda paylaşacağım. Bu programı test amaçlı kullandım. Üzerinde çeşitli düzenlemeler yaptığım için optimize bir halde değil ve hatalar olabilir. Bunları göz ardı edip kendinize göre düzenleyebilirsiniz. Son olarak hesapladığımız katsayılar içerisindeki detayı görebiliyor musun ? “Dikkatli bakıyor musun ?”

Are you watching closely?

Bir sonraki yazıda görüşmek üzere. Esen kalın.

Özel Teşekkür;

Python konusunda gece gündüz bunaltıcı sorularıma cevap vererek hiç bir desteğini esirgemeyen sayın Muhittin KAPLAN hocama bir teşekkürü borç bilirim.