FPGA Günlükleri – 8 Bit Multiplexer
Bir çok dijital devrede birden fazla sinyal arasından birini seçip ilgili yere yönlendirmek adına kullanılan Multiplexer yani Çoklayıcılar çok fazla kullanacağımız yapılar. Bu yapıları “Seçici” dendiğini de duyabilirsiniz. Teori oldukça basit. Giriş sinyalleri X(n) olsun. Çıkış sinyali Y olur. Seçim sinyallari ise S() ile belirtelim. Örnek olarak 2 adet giriş sinyalinde birini çıkışa yönlendirmek için 1 adet S() sinyali gerekir. 4 Giriş varsa bundan birini seçmek için 2 Sinyal gerekir. Yani 2^s = x olarak formül haline gelir. MUX tasarımında temel başlangıç için tüm x ve s durumlarını yazarız. 8 Bit için çok fazla yacağız gibi. Merak etmeyin bir kestirme biliyorum. Hadi başlayalım.
2×1 Multiplexer
Önce 2 Bitlik MUX yapısını anlayarak başlamakta fayda var. 2 Bit MUX için 2 adet giriş ve 1 adet seçim girişi vardır. Yapısı şu şekilde gösterilebilir.
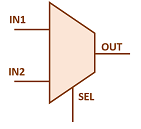
Çalışma mantığını açıklayan GIF ile anlaşılması oldukça kolay.
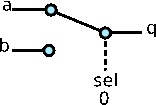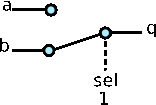
Her bir seçim ve giriş durumları için tabloyu yazarsak doğruluk tablosunu elde edebiliriz.
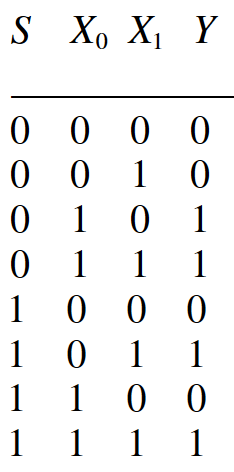
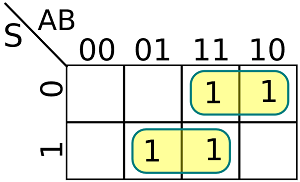
Karnaugh haritası ise şu şekilde olur.
Dijital tasarımı elde edelim.
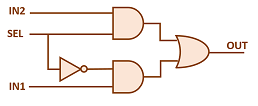
Gördüğünüz üzere 2×1 MUX basit. Bunun VHDL karşılığı şu şekilde.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
library IEEE; use IEEE.STD_LOGIC_1164.all; entity Multiplexer is port ( X0 : in STD_LOGIC; X1 : in STD_LOGIC; S : in STD_LOGIC; Y : out STD_LOGIC ); end Multiplexer; architecture karakter of Multiplexer is begin Y <= (S and X1) or (not(S) and X0); end karakter; |
Eminim 2×1 fazla işimize yaramayacak bize daha büyük olanı gerekiyor. Yavaş yavaş büyüterek bu büyümenin mantığını kavrayalım. Sırada 4×1 var fakat aynı adımları yapmayacağım sadece blok olarak göstereceğim çünkü diğer adımları öğrendik.
4×1 Multiplexer
4×1 MUX aslında 2 Adet 2×1 MUX’un çıkışlarının seçimlerinden oluşur. Yani seçimlerin seçimidir. Doğruluk tablosunu ve VHDL kısmını size bırakıyorum.
Bu yapının boolean eşitliğini bütün MUX’ları açarak bulabilirsiniz fakat direk olarak MUX’lara isim verip yaparsanız daha kolay olacaktır.
Boolean Eşitliği şu şekildedir. (I(n) = X(n))
8×1 Multiplexer
Şimdi sırada 8×1 var bunuda yaptığımızda yapının nasıl ilerlediği kafanıza oturacaktır. dikey olarak ilk sıraya S(0) ikinci kolona S(1) ve S(2) şeklinde ilerlediğini göreceksiniz.
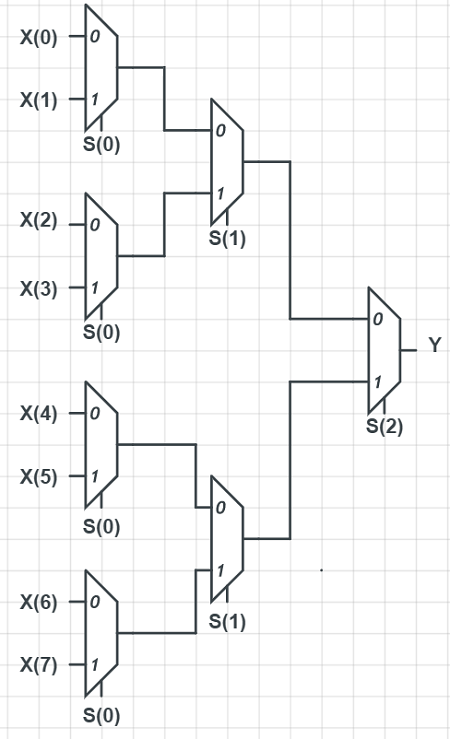
Boolean Eşitliği şu şekildedir. (I(n) = X(n))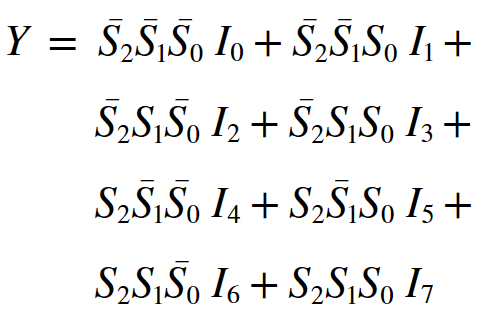
VHDL Kodu :
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
library IEEE; use IEEE.STD_LOGIC_1164.all; entity Multiplexer is port ( X : in STD_LOGIC_VECTOR (7 downto 0); S : in STD_LOGIC_VECTOR (2 downto 0); Y : out STD_LOGIC ); end Multiplexer; architecture karakter of Multiplexer is begin Y <= (X(0) and not(S(2)) and not(S(1)) and not(S(0))) or (X(1) and not(S(2)) and not(S(1)) and S(0)) or (X(2) and not(S(2)) and S(1) and not(S(0))) or (X(3) and S(2) and not(S(1)) and S(0)) or (X(4) and S(2) and not(S(1)) and not(S(0))) or (X(5) and not(S(2)) and S(1) and S(0)) or (X(6) and not(S(2)) and not(S(1)) and S(0)) or (X(7) and S(2) and S(1) and S(0)); end karakter; |
VHDL kısmında bir öncekilere göre ekstra kullandığım şu kod kolaylık sağlıyor.
|
1 |
S : in STD_LOGIC_VECTOR (2 downto 0); |
Bu bize S sinyalinin 3 adet’lik bir hat olduğunu tanımlama şansı veriyor. Alt alta teker teker yazma zahmetine girmiyoruz. Elemanlarına ulaşmak için ise şu şekilde kullanıyoruz.
|
1 2 3 |
S(0) S(1) S(2) |
Kodu henüz test etmedim. 8 giriş ve 3 tane seçim için kablo takmaya üşendim. 🙂 Simülasyon yapmayı da henüz öğrenmedim. Buda bir başka yazının konusu olsun. Şimdilik bu kadar.
Esen kalın.
Son yorumlar