İstenmeyene Göğüs Gerenler : Filtreler – 2 – Bilinear Z Transform (Tustin Transform)

Yine bolca matematik içeren bu yazıda filtrelerin dijital hallerine giriş yapacağız. Özellikle dijital kontrolün kalbi olan bu filtreler beraberinde çözülmesi gereken bir takım sorunları da yanında getirecek. Bir analog filtrenin dijital karşılığını modelleyeceğimiz bu yazının aklımızdaki bir çok soru işaretini gidereceğini düşünüyorum. Matematiksel dönüşümler, bilgisayar analizleri ve programlama kısmında yapılan optimizasyonlar gibi konulara da değineceğimiz bu yazıda yapılacak çok iş var. Hazırsanız başlayalım.

Giriş

Öncelikle ortadaki problemi belirleyelim. Bu problem analog devrelerde kullandığımız filtrelerin dijital ortamlarda modellenebilmesi. Biraz daha açacak olursak amacımız R-L-C gibi elemanlar ile tasarlanan analog filtrelerin dijital ortamlardaki karşılığını oluşturmak. Bildiğiniz üzere R-L-C gibi elemanların henüz bir dijital karşılığını bilmiyoruz. Bu elemanların matematiksel karşılıklarını bulabilirsek sayısal ortamlarda filtreleri gerçekleyebiliriz. Öncelikle örneklerimizi pasif RC filtreler üzerinden yapacağımızı belirtelim. Öğreneceğimiz teknik ile daha sonra bir çok analog modeli sayısal ortama taşıyabileceğimiz düşünüyorum. İşe Laplace dönüşümünü kullanarak başlayacağız. Bir önceki yazıda alçak geçiren filtrenin S düzlemindeki karşılığını bulmuştuk bu yüzden bu adımları tekrar etmeyeceğim. S düzleminde bu basit işi anlayıp tamamladıysanız artık Z düzlemine geçebiliriz. Burada kullanacağımız yapının adı literatürde “Bilinear Z Transform” olarak geçiyor. Aslında daha az bilinen adıyla “Tustin Transform” olarak da görebilirsiniz. S düzleminde Z düzlemine yapacağımız bu çok sert geçişte bilmemiz gerek S yerine ne yazacağımızdır.  Bilinear Z Dönüşümü bize S yerine aşağıdaki ifadeyi yazmamızı söyler.

Bilinear Z Dönüşümü

$$s = \frac{1}{T} \cdot \left (\frac{1-z^{-1}}{1+z^{-1}}\right )$$

Bu ifadenin nereden geldiğini aslında çok bellidir. Klasik z dönüşüm ifadesi yazılırsa bilinear dönüşüm ifadesine ulaşabiliriz.

$$z = {e}^{sT}$$

Burada s ifadesini çekecek olursak;

$$\ln(z) = \ln ({e}^{sT})$$

$$\ln(z) = sT \cdot \ln(e)$$

$$\ln(z) = sT$$

$$s = \frac{ln(z)}{T}$$

Ayrık zamanda çalışırken logaritmik bir ifade yerine cebirsel ifade olmasını isteriz. Bu yüzden $ln(z)$ gibi zor hesaplanan bir fonksiyon yerine bir açılım kullanmak kaçınılmaz olacaktır. Sonsuz seri ifadelerinde bilineari ele alacak olursak sadece ilk bileşen yani birinci derece ifade olarak kullanıldığı görülür.

$$\ln(z) = 2\left [\left ({z-1 \over z+1}\right )+ {1\over3} \left({z-1\over z+1}\right)^3+ {1\over5} \left({z-1\over z+1}\right)^5 +\cdots\right],$$

İlk bileşeni aldığımızda tam anlamıyla bilinear dönüşümü elde etmiş oluruz. Burada s ve z arasındaki bağlantının bir eşitlik değil yakınsama olduğu unutulmamalı.

$$s \approx \frac{2}{T} \cdot \left (\frac{z-1}{z+1}\right )$$

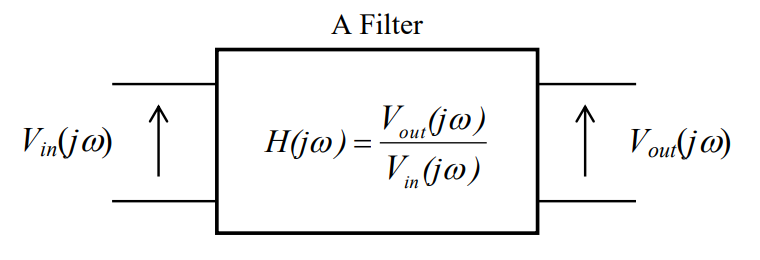
Burada T bizim örnekleme periyodudur. Cebirsel açıdan bizi uğraştıracak gibi gözükse de transfer fonksiyonlarında V(s), Z düzlemine direk olarak V(z) olarak geçmektedir. İlk örneğe bir alçak geçiren pasif RC filtre ile başlayalım.

$$T(s) = \frac{V_{out}(s)}{V_{in}(s)} = \frac{1}{1+sRC}$$

S yerine yukarıdaki özdeşliği yazalım.

$$\frac{V_{out}(z)}{V_{in}(z)} = \frac{1}{1+\frac{2}{T}\frac{(1-z^{-1})}{(1+z^{-1})}RC}$$

Asıl işlemler burada başlıyor. Bu noktada aradığımız şey şu tarzda bir denklem.

$$\displaylines{V_{out}(z) = a_{0}V_{in}(z)+a_{1}V_{in}(z)z^{-1}+a_{2}V_{in}(z)z^{-2}+\ … \\ +\ b_{0}V_{out}(z)+b_{1}V_{out}(z)z^{-1}+b_{2}V_{out}z^{-2}+\ …}$$

Asıl işlemler burada başlıyor. Bu noktada aradığımız şey şu tarzda bir denklem.

Aradığımız bu denklemin sağ tarafında Vo(z) olması şart değil fakat Vin(z) olması gerekiyor. Gerekli cebirsel düzenlemeleri buna göre yapmalıyız. Gerekli işlemleri aşağıda yaptım ve sonunda aradığımız tarzda bir denklem elde ettim.

$$\frac{V_{out}(z)}{V_{in}(z)} = \frac{1}{1+\frac{2}{T}\frac{(1-z^{-1})}{(1+z^{-1})}RC}$$

$$\frac{V_{out}(z)}{V_{in}(z)} = \frac{T(1+z^{-1})}{T(1+z^{-1})+2RC(1-z^{-1})}$$

$$\frac{V_{out}(z)}{V_{in}(z)} = \frac{T+Tz^{-1}}{T+Tz^{-1}+2RC-2RCz^{-1}}$$

$$\frac{V_{out}(z)}{V_{in}(z)} = \frac{T+Tz^{-1}}{(T+2RC)+z^{-1}(T-2RC)}$$

$$V_{out}(z)((T+2RC)+z^{-1}(T-2RC)) =V_{in}(z)(T+Tz^{-1})$$

$$V_{out}(z)((T+2RC)+z^{-1}(T-2RC)) =V_{in}(z)T+V_{in}(z)Tz^{-1}$$

$$V_{out}(z)(T+2RC)+V_{out}(z)(T-2RC)z^{-1} =V_{in}(z)T+V_{in}(z)Tz^{-1}$$

$$V_{out}(z)(T+2RC) =V_{in}(z)T+V_{in}(z)Tz^{-1}-V_{out}(z)(T-2RC)z^{-1}$$

$$V_{out}(z)=\frac{V_{in}(z)T+V_{in}(z)Tz^{-1}-V_{out}(z)(T-2RC)z^{-1}}{(T+2RC)}$$

$$V_{out}(z)=\frac{V_{in}(z)T}{(T+2RC)}+\frac{V_{in}(z)Tz^{-1}}{(T+2RC)}-\frac{V_{out}(z)(T-2RC)z^{-1}}{(T+2RC)}$$

$$V_{out}(z)=V_{in}(z)\frac{T}{T+2RC}+V_{in}(z)z^{-1}\frac{T}{T+2RC}-V_{out}(z)z^{-1}\frac{T-2RC}{T+2RC}$$

Bu noktada artık ayrık zamana geçebiliriz.

$$\displaylines{V_{out}(z) = y\left[n\right] \\ V_{in}(z) = x\left[n\right] \\ V_{out}(z)z^{-1} = y\left[n-1\right] \\ V_{in}(z)z^{-1} = x\left[n-1\right] \\ V_{out}(z)z^{-k} = y\left[n-k\right] \\ V_{in}(z)z^{-k} = x\left[n-k\right]}$$

Bu eşitlikleri yerine yazdığımızda şunu elde ederiz.

$$y\left[n\right] = x\left[n\right]\frac{T}{T+2RC}+x\left[n-1\right]\frac{T}{T+2RC}-y\left[n-1\right]\frac{T-2RC}{T+2RC}$$

Burada $y[n]$ çıkış değeri, $x[n]$ filtrelenecek değerlerdir. Bu denklemi yazılıma ekleyip uygun RC değerleri vererek istediğiniz frekansı elde edip filtreleme işlemini yapabilirsiniz.

“Complementary Filter” Kavramının Gizemi

Bir sonraki aşamaya geçmeden önce burada çok önemli olduğunu düşündüğün bir noktaya değinmek istiyorum. Elde ettiğiniz denklemde çalışmanın basit olması adına bazı değişken dönüşümleri yapalım.

$$ \alpha = \frac{T}{T+2RC} \,\,\,\,\, \beta= \frac{T-2RC}{T+2RC}$$

$$ y\left[n\right] = \alpha \cdot x\left[n\right]+\alpha\cdot x\left[n-1\right]-\beta \cdot y\left[n-1\right]$$

Peki giriş değeri olan $x [n]$ bir önce ki giriş olan $x [n-1]$’e çok yakın olduğu varsayımı yapılırsa ne olur? Eğer örnekleme sinyali yüksek ise neredeyse aynı oldukları kabul edilebilir öyle değil mi?

$$x [n] \approx x [n-1]$$

O halde denklemi yeniden düzenlersek aşağıdaki ifadeyi elde ederiz.

$$ y\left[n\right] \approx 2\alpha \cdot x\left[n\right]-\beta\cdot y\left[n-1\right]$$

Denklem oldukça sadeleşti fakat $\alpha$ ile $\beta$ arasında başka bir bağlantı olduğu gözüküyor.

$$2\alpha = \frac{2T}{T+2RC}$$

$$\beta + 1 = \frac{T-2RC}{T+2RC} + \frac{T+2RC}{T+2RC} = \frac{T-2RC+T+2RC}{T+2RC} = \frac{2T}{T+2RC}$$

$$2\alpha = \beta + 1$$

Bu ilişki yazıldıktan sonra denklemin yeni halini yazalım.

$$ y\left[n\right] \approx (\beta + 1)\cdot x\left[n\right]-\beta \cdot y\left[n-1\right]$$

Son değişken dönüşümünü yaparak ifadeyi biraz daha basitleştirelim;

$$\gamma = 1+\beta$$

$$ y\left[n\right] \approx \gamma\cdot x\left[n\right]+(1-\gamma) \cdot y\left[n-1\right]$$

Görüldüğü üzere katsayıları arasındaki ilişki sadece tümleyen olduğundan kalman filtresi yerine kullanılan o meşhur “Complementary Filtresi” bu şekilde doğmuş oldu. Tümleyen filtresinin aslında birinci dereceden alçak geçiren bir filtre olduğu buradan anlaşılmış oldu.

Python Uygulaması

Ben Python dilinde gerekli testleri yaptım. Hazır matematiksel fonksiyonlar, tek satırda FFT işlemini gibi kolaylıklar ile analiz için hızlı bir çözüm sunan Python, arayüz açısından da QT Designer ile birlikte gayet başarılı çıktılar verebiliyor.

Test Değerleri;

• $R =1 k\Omega$
• $C = 100nF$
• Örnek Sayısı $(T_{s}) = 8192$
• $T_{s} = \frac{1}{8192} = 0.00012207031$
• Giriş Sinyali : $V_{in}(t)=sin(2 \cdot \pi \cdot f\cdot t)$
• $f_{cutoff} \approx 1.6 kHz = \frac{1}{2\cdot\pi\cdot R\cdot C}$

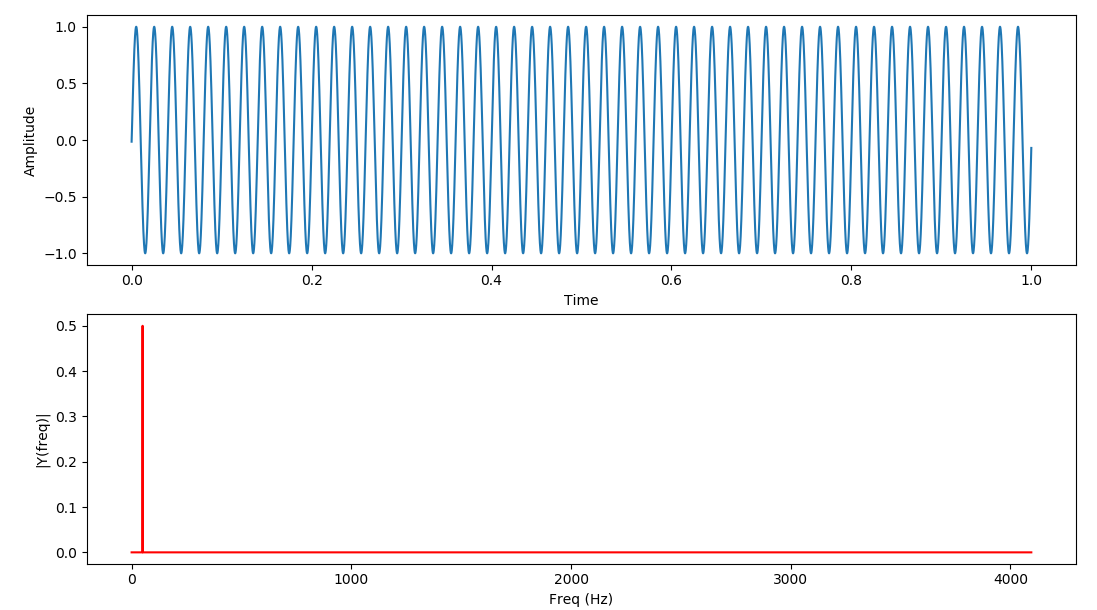
Giriş sinyalinin frekansı 50 Hz için;

Giriş sinyalinin frekansı 1 kHz için;

Bu noktada filtrenin devreye girmeye başladığını ve genliğin düşmeye başladığını görebilirsiniz. Ayrıca FFT çıktısında ki büyüklük normal sinyalin genliğinin yarısıdır. FFT işleminde sadece pozitif değerleri aldık.

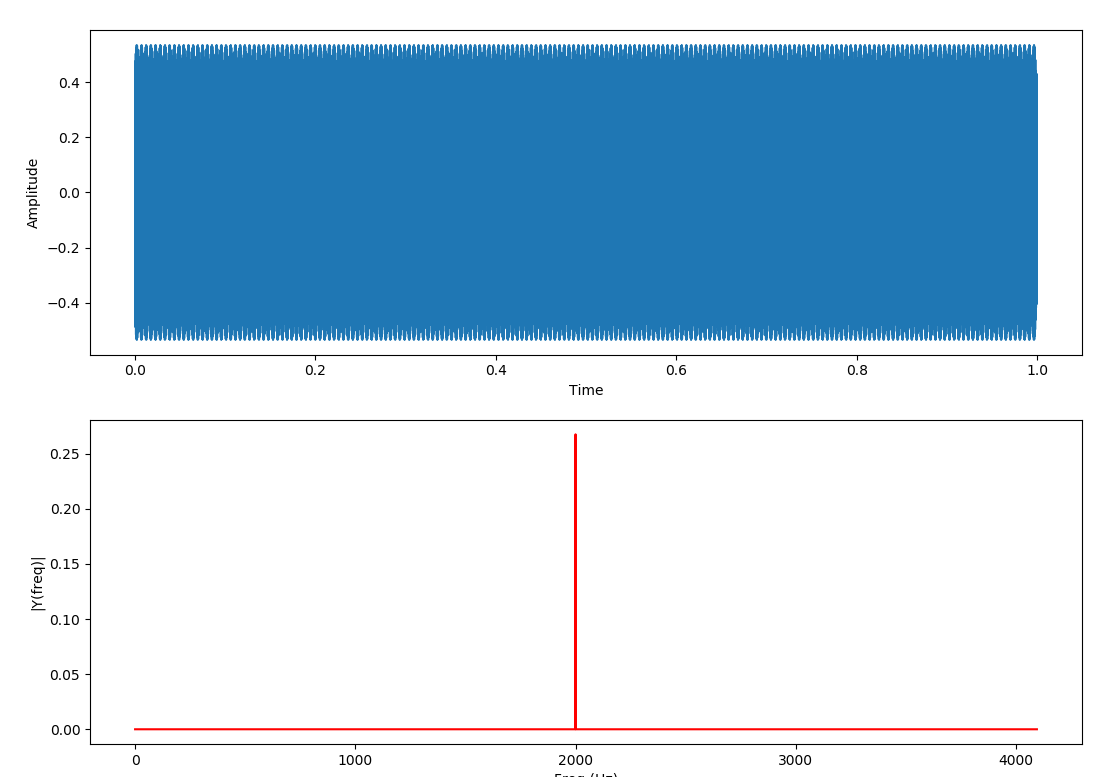
Giriş sinyalinin frekansı 2 kHz için;

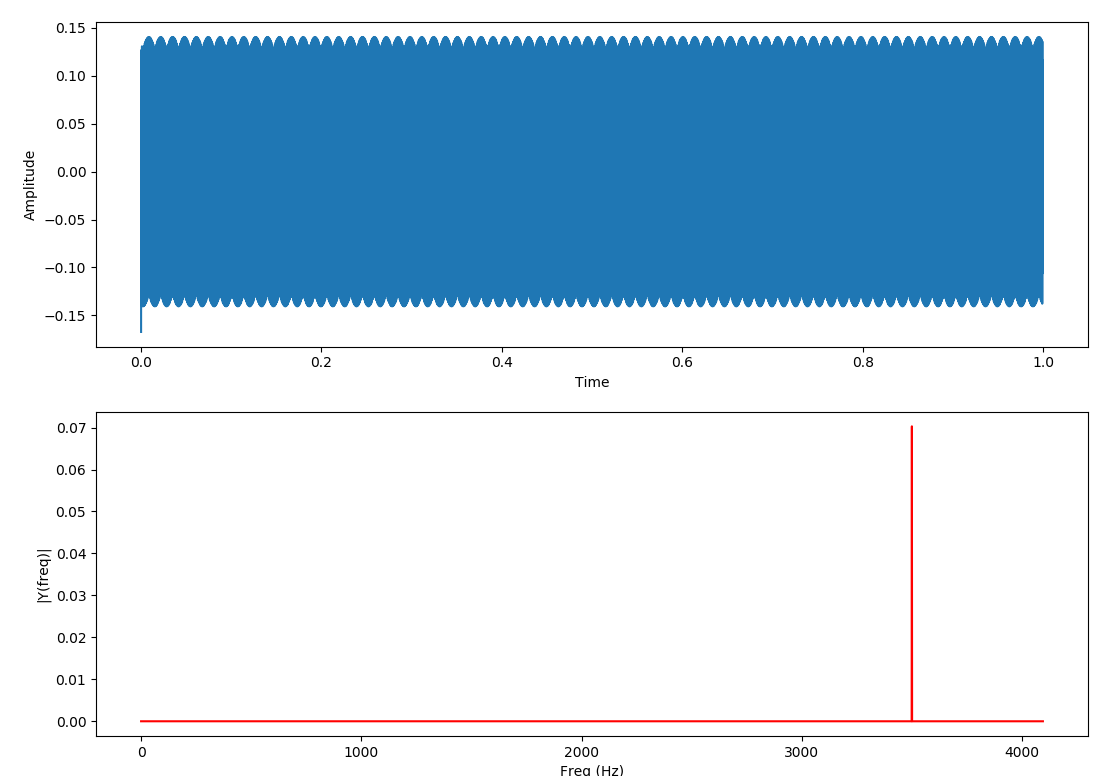
Son olarak 3.5 kHz için çıktıyı görelim.

Görüldüğü gibi 3.5kHz için genlik yaklaşık olarak 0.14 civarı. Dahaya yüksek değerler için bileşen iyice bastırılmaya başlayıp akabinde çok küçülüp yok olacak. Şimdi 3 bileşenli bir sinyali test edelim.

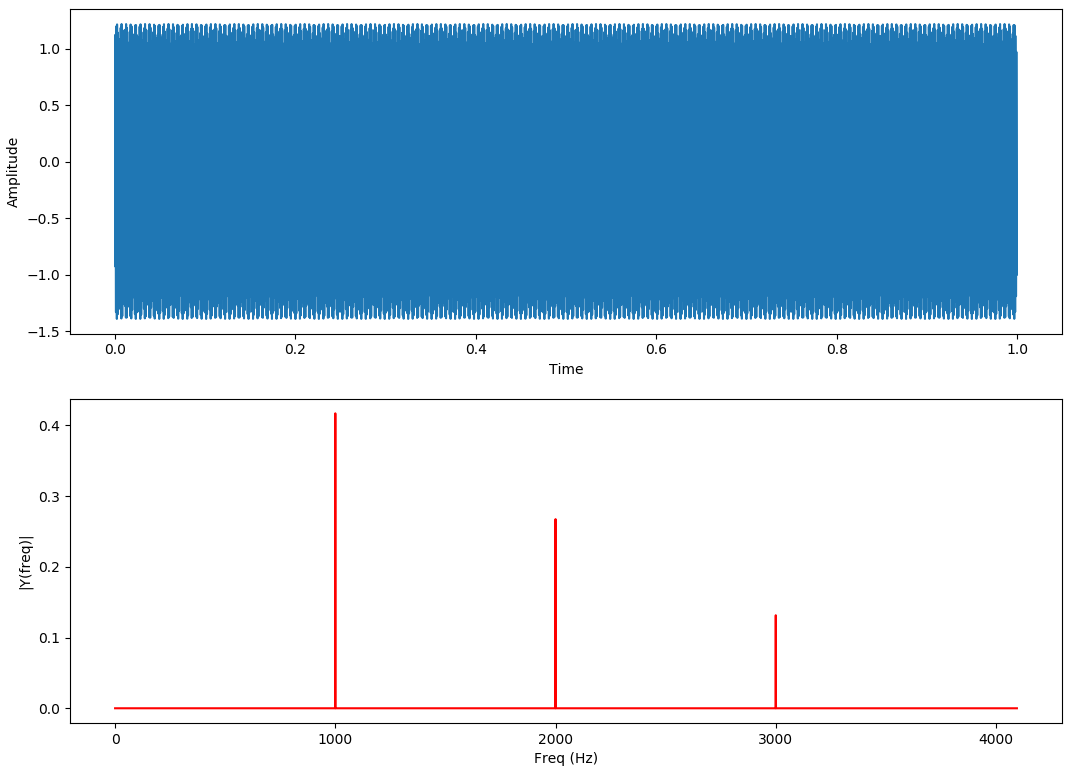
Giriş sinyali;

$$V_{in}(t)=sin(2\cdot\pi\cdot1000\cdot t) + sin(2\cdot\pi\cdot2000\cdot t) + sin(2\cdot\pi\cdot3000\cdot t)$$

Her şey yolunda gözüküyor değil mi ? Öyle gözükse de şuan anlayamadığımız bir problem var.

Bilinear Z dönüşümünde “Frequency Warping” denen bir problem mevcut. Bu sorun yüksek frekanslarda daha çok görülür. “Frequency Warping” denen kavram aslında istediğimiz analog filtrenin kesim frekansının dijital ortama taşınınca bozulmasıdır diyebiliriz. Güzel haber bu bozulma hesaplanabilir.

$$\displaylines{Frequency\ Warping \\ \omega_{a}=Analog\ Angular \ Frequency \\ \omega_{d}=Digital\ Angular \ Frequency \\ \omega_{a} = \frac{2}{T}\tan(\frac{\omega_{d}T}{2})}$$

Burada dijital frekansı bulabilmek içi ters dönüşüm uygulayalım. Unutmadan burada frekansların açısal frekans olduğunu unutmayın. Ayrıca hesaplamaları yaparken Derece-Radyan moduna dikkat edin.

$$\arctan{\left(\omega_{a}\frac{T}{2}\right)}=\arctan\left(\tan\left(\omega_{d}\frac{T}{2}\right)\right)$$

$$\arctan{\left(\omega_{a}\frac{T}{2}\right)}=\omega_{d}\frac{T}{2}$$

$$\frac{2}{T}\arctan{\left(\omega_{a}\frac{T}{2}\right)}=\omega_{d}$$

$$f_{d} = \frac{1}{\pi T }\arctan{\left(\pi Tf_{a}\right)}$$

Uygulamasını yaptığımız $T_{s} = \frac{1}{8192}$ ve $f_{cutoff} \approx 1.6$ kHz için analog frekansımızı yerine yazdığımızda dijital frekansı 1428.95 yani ~ 1.42 kHz olarak buluruz. İki değer arasında yaklaşık olarak 163 Hz var. Bu değer küçük frekanslarda göz ardı edilebilecek olsa bile büyük frekanslarda istenmeyen hata paylarının oluşmasına sebep olur. Bu yüzden hesaplamaları yaparken bu formülü dikkate almak gerekir.

Bu işi yapan Python kodu aşağıdadır.

Sonuç

Özellikle filtrenin katsayılarına dikkat edecek olursanız MCU gibi yapılarda bu katsayıların optimize edilmesi gerekiyor. Çünkü hız sinyal işlemede en önemli faktördür. İşlemcinin Fixed yada Floating point olması durumuna göre farklı optimizasyonlar gerekebilir. İlerleyen yazılarda bir uygulama yapmayı planlıyorum. FIR-IIR gibi bir çok başlık altında tonlarca filtre çeşidi var. Zamanı geldikçe hepsine teker teker gireceğiz ve böylece kafalardaki soru işaretlerini gidereceğiz. Şimdilik bu kadar.

Esen kalın.

Kaynaklar

http://julien.elfa-systemes.com/perso/%234.1.%20Digital%20filter.pdf