N. Dereceden Polinomun Kökleri : Bairstow’s Method

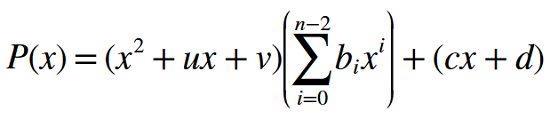
Her şey 2 hafta önce girdiğim “Sayısal Çözüm Yöntemleri” dersinde hocamın “n. dereceden bir polinomun tüm köklerini bulacağız.” demesiyle başladı. Şimdi bu cümlede 3 tane gizli ayrıntı var. Bunlardan ilki bu işleri tamamen nümerik tekniklerle yapacak olmamız. Bu ilk adım pek kafamızı karıştırmıyor çünkü aklımıza ilk gelen yöntem, bir epsilon hatasına kadar döngüyü tekrarlamak.

İkincisi bu kökler içinde sanal köklerinde barınacağı. Bu bizim için sorun değil bunun sebebi kompleks köklerin formülünü biliyor olmamız. Gördüğünüz gibi hala korkacak bir şey yok!

Üçüncüsü ve benim kafam en çok meşgul eden ise bu polinomun derecesinin sabit değil n. dereceden olması! Evet bu cümlenin arkasında yatan zorluğun ne olduğunu şimdi rahatça görebiliyoruz dimi? Bazı dereceleri hesaplamak kolay. Mesela 1, 2, 3 hadi 4 olsun. Peki 10, 15 hatta 50. derece olduğunu düşünün. Kısacası bize n. dereceden bir polinomun tüm köklerini bulan çok güçlü bir algoritma gerekiyor. Merak etmeyin bunu yapan bir matematiksel modele sahibiz. Bu modeli geliştiren Leonard Bairstow’a bir teşekkürü borç biliriz. O halde hazırsanız Bay Bairstow’un bu ulvi matematiksel modelini biraz olsun inceleyerek anlamaya çalışalım. Hatta bunu yazılımsal hale getirip işleri daha kolaylaştıralım!

Öncelikle tekniğin felsefesinden bahsedecek olursak n. dereceden bir polinomun 2. dereceden bir polinoma bölünmesiyle ana polinomun derecesinin düşürülmesine dayanıyor. Bu bölme işlemi devam edilerek köklerin bölünmesi daha kolay bir hal alıyor. Bu size polinom bölmesini hatırlatmalı. Burada bölme işini uzun bölme olarak değil sentetik bölme olarak yapıyoruz. Bu bölme işleminde bir kalan olabileceğini de unutmayın. Temel matematik yapısı aşağıdaki gibi.

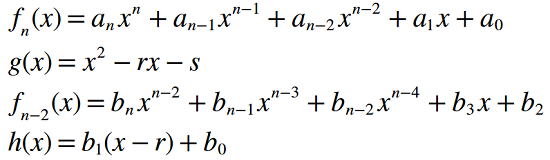
Burada h(x) kalan olmaktadır. Katsayılar arasındaki bağıntı ise şu şekildedir.

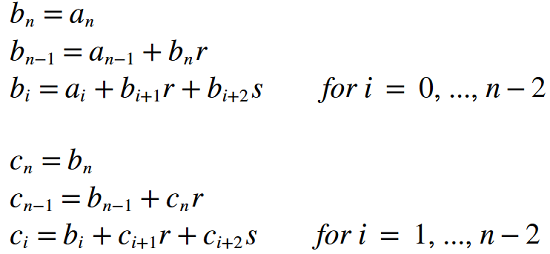
Bu adımlardan sonra delta r ve delta s değerleri bize her döngüde yeni bir girdi verecek ve köklere yakınsamayı sağlayacak.

Önemli Not : İlk girilen r ve s değerleri tamamen keyfidir. Bu sizin kökleri bulma işinizi belki kolaylaştırabilir. Eğer ilk gerçek r ve s değerlerine yakın bir değer tahmininde bulunup bu değerleri yazarsanız, ilk kökleri elde etme süreniz kısalabilir. Bu durum tamamen şansınıza kalmıştır. Bu yüzden r ve s değerlerinin başlangıç değerlerine kafa yormaya gerek yoktur. Bazı kaynaklar bu r ve s değerlerini a dizisinden eleman seçerek başlatır. Bu durumunda keyfi olduğunu unutmayın.

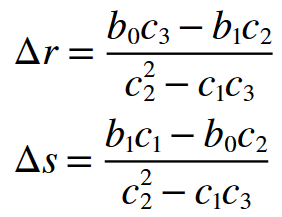
Bu adımdan sonra r ve s değerlerini ne kadar değiştireceğimizi elde ediyoruz. Bu işlemi belirlediğimiz bir “Epsilon” hata payına kadar yaparak kökleri elde edebiliriz. Bence daha fazla matematiğe girmeden yazılım kısmına geçelim. Eğer bu işin arkasındaki matematiğe girmek istiyorsanız internette bulabileceğiniz güzel makaleler ver. Bu metodun arkasında yatan matematik, içerdiği Taylor açılımına ve Kısmi Türeve bakacak olursak pek küçük değil. Ben bu işlemleri hem Python hemde Matlab ortamında gerçekleştirdim ve sonuçları Matlab’ın kendi “roots” fonksiyonu ile karşılaştırdım. Aşağıda hazırladığım basit bir Python programını görebilirsiniz.

Her dereceye uygun olsun diye yazılıma 2. ve 1. dereceleri hesaplama özelliğini de ekledim. Bu metot şu şekilde kullanılabilir. Polinom katsayılarının 0’dan n’ye gittiğine dikkat edin.

Gördüğünüz üzere artık elimizde N. dereceden bir polinomun tüm köklerini hesaplayan bir algoritma var. Hemde kompleks kökleri bile hesaplayabiliyor! Tabi siz dünyalılar bunu “Matlab varken neden bu algoritma ile uğraştık?” şeklinde sorgulayabilirsiniz. Belki bir gün bunu anlatan bir yazı yazarım.

Kim bilir, belki yarın, belki yarından da yakın.

Projeye Github hesabımdan ulaşabilirsiniz.

Esen kalın.