Sinsi Bir İntegrasyon Tekniği : Weierstrass Substitution

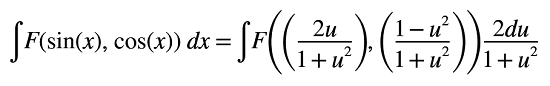Bildiğiniz üzere mühendisin en güçlü silahı olan matematik, beraberinde bir takım güçlükler getirir. Bunlar kimi zaman diferansiyel denklemler, kimi zaman ise gördüğümüzde elimizi kolumuzu bağlayan integral problemleri olur. Üzerinde duracağımız integral problemleri için genellikle fazla bilinmeyen ve üniversitede kısaca görülen “Weierstrass Substitution” tekniği, trigonometrik ifadeler içeren integral problemlerini çözmek adına büyük bir silah olarak kullanılır. İçerisinde bir veya birden fazla trigonometrik ifade bulunduran ve oldukça basit gözüken bir takım integral problemlerini çözmeye çalıştığınızda göreceksiniz ki elinizde bildiğiniz bir çözüm tekniği kalmayacak. Merak etmeyin küçük bir joker hakkınız var. Hadi gelin ve birlikte bu enteresan gizli silahı keşfedelim.

Öncelikle şu alıntıyı araya ilave etmek istiyorum;

Michael Spivak wrote that “The world’s sneakiest substitution is undoubtedly this technique”

Konunun felsefesinde bulunan teknik kısaca şu; “Trigonometrik ifadeleri cebirsel hallere dönüştürüp, integral problemini çözdükten sonra tekrar trigonometrik ifadeye dönüştürmek.”

Özellikle payda kısmında sabit sayılarla bir arada karşımıza sıkça çıkan bu yapıyı çözümlemek için öncesinde bir takım tanımlamalara ihtiyaç duyuyoruz. Yapacağımız tanımlamalardan önce şu dönüşümü yapmak gerekiyor.

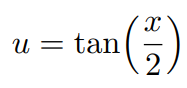
Bu yüzden bu konuyu “Tangent half-angle substitution” başlığı olarak da görebilirsiniz. Peki sin ve cos gibi diğer trigonometrik ifadelere nasıl bir karşılık vereceğiz? Bu noktada cebirsel metotlar ile ilerleyebilirsiniz fakat ilgili değerler elimizde olduğundan dolayı üçgen çizip sin(x) ve cos(x) fonksiyonlarının karşılıklarını daha rahat bulabilirsiniz.

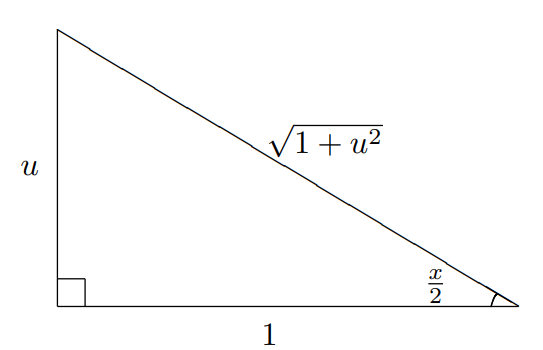
Buradan sin(x) ve cos(x) ifadelerini bulabilmek için aşağıdaki özdeşliklerden faydalanalım.

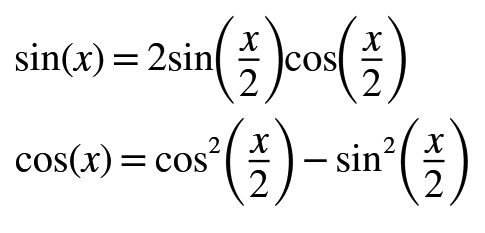
Yukarıdaki üçgenden sin(x/2) ve cos(x/2) fonksiyonlarını çekelim ve ardından üstteki özdeşlik de yerine yazarak sin(x) ve cos(x) değerlerini bulalım.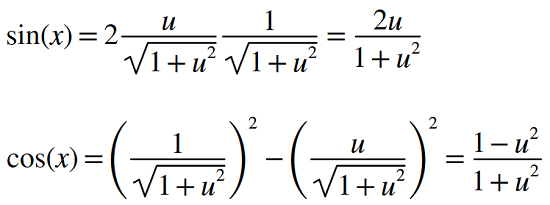

Artık elimizde temel trigonometrik fonksiyonlar için bir cebirsel karşılık var. Bu aşamadan sonra tek ihtiyacımız olan şey integral deki dx ifadesine nasıl bir kaşılık bulacağımız. Bunu da başlangıçta yaptığımız u = tan(x/2) ifadesinin türevini alarak bulabiliriz. Bu işlemi klasik “değişken(u) dönüşümü” olarak da biliyoruz.

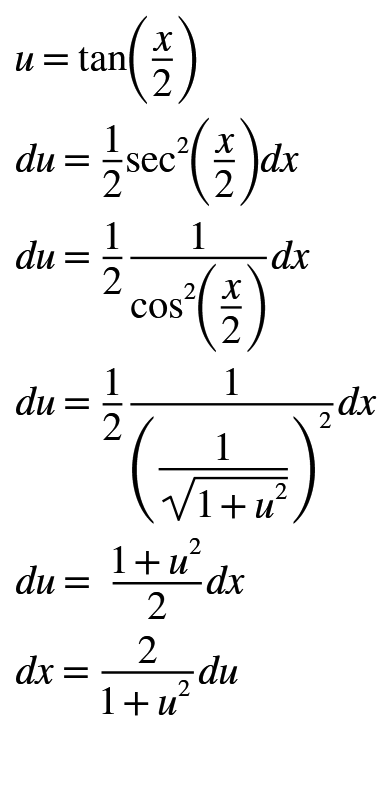
Artık elimizde bütün ifadeler mevcut. Diğer trigonometrik fonksiyonlar için bu özdeşliklerden yola çıkıp devam edebilirsiniz. Konuyu özetlemek adına dx/(1+cos(x)) integral problemini çözelim.

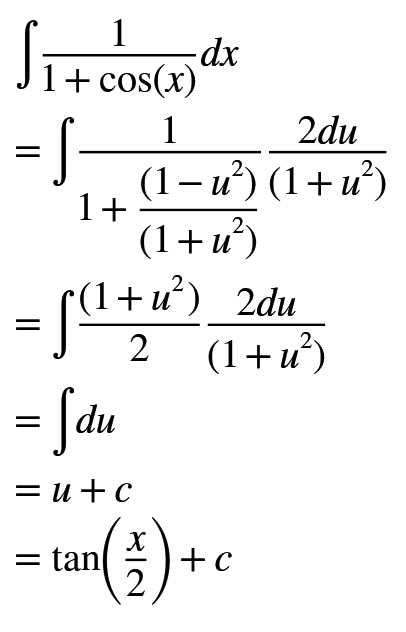
Yukarıda görüldüğü üzere problem çok basit bir cebirsel hale dönüştürülerek çözüldü. Burada örnek soru farklı yollar ile daha kolay çözülebilir fakat bu ifadeye başka fonksiyonlar eklediğinizde çözüm çok zorlaşabilir. Bu konuyu pekiştirmek adına verdiğim basit bir örnek. Bir adım daha öteye giderek sec(x) integral problemini çözmeye odaklanalım.

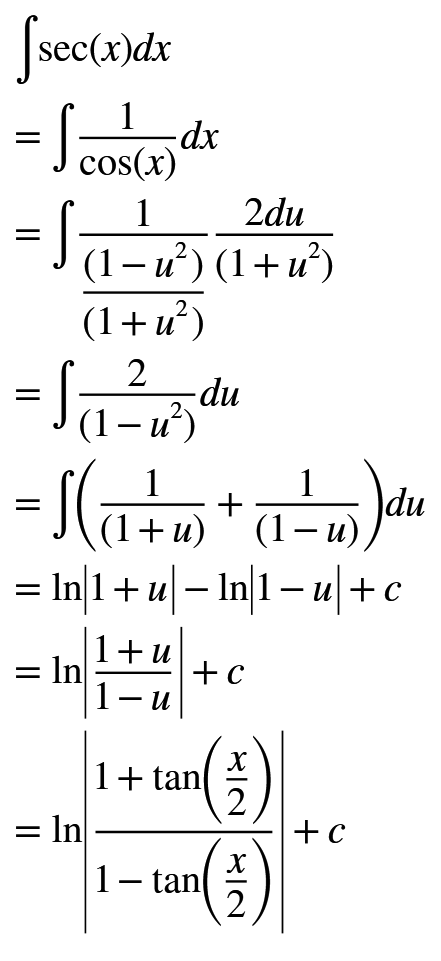Yine görüldüğü üzere trigonometrik fonksiyon içeren integral problemleri”Weierstrass Substitution” tekniği ile kolayca çözülebilmektedir. Buna benzer yüzlerce örnek verebiliriz. Bir takım alıştırmalar yapmak ve konuyu pekiştirmek adına “Calculus” kitapları üzerinden çalışma yapabilirsiniz. Ayrıca özel integrasyon tekniklerini anlatan kitapları da inceleyerek özel çözüm tekniklerini öğrenmek mümkün.

Esen kalın.