Sinyallerimdeki Şeytanlar – Fourier Transform
Bu yazıda Joseph Fourier’in bulduğu “Fourier Dönüşümü” adlı, bir hayli ilginç olan ve mühendislik öğrencilerinin birlikte yatıp kalktığı bu konuya giriş yapacağız. Bu konuya girmeden önce üzerine düşüneceğimiz başka bir problem var. Normal de sinyallerimizi zaman bağlı örnekler ve bunları işlemek için uğraşırız. Zamana bağlı bir sinyalde bildiğiniz üzere sadece (t) anındaki (Genliği) elde edebiliriz. Geometrik olarak bir x(t) değerine karşın bir y(Genlik) değeri olur. Bu oldukça basit öyle değil mi ? Şimdi asıl soruna gelelim. Elimizdeki sinyalin içinde hangi frekans bileşenlerinin olduğunu öğrenmek isteydik ne yapacaktık ? Koordinat düzleminde x yerine frekans’ın olmasını istiyoruz. O halde frekans düzlemine ışınlanalım !
Joseph Fourier’in yaptığı en mükemmel çalışmalardan biri olan “Fourier Serileri” ve “Fourier Dönüşümü” gibi konular bizim bir çok sorumuzu yanıtlayacak. Bu işin matematiğine çok daha derin olarak başka bir yazı serisinde gireceğim fakat şuan işin matematik değil mühendislik tarafındayız. Hadi gelin Joseph Fourier’in bulduğu Fourier Dönüşümü formülünü inceleyip uygulayalım.
$$\displaylines{\mathscr{F(\omega)} = \int_{- \infty }^{\infty} f(t) e^{-j\omega t}dt \\ f(t) = \frac{1}{2\pi}\int_{- \infty }^{\infty} \mathscr{F(\omega)} e^{j\omega t}d\omega}$$
Her şey harika artık fonksiyonumuzu frekans eksenine götürecek hatta geri getirecek formüllerimiz var. Sağ olsun sevgili Joseph bu işlemleri bizim için yapmış fakat hala bir problemimiz var. Mühendislik uygulaması yaptığımız taktirde sinyalimizi periyodik olarak örnekleriz yani kağıtta olduğu gibi elimizde kesin fonksiyonlar yoktur. Bu yüzden sonsuz küçük zamanlı toplamları yani integral yapılarını ne yazık ki kullanamayız. Aslında bize bu formülün sonsuz değilde sonlu toplam olacak şekilde bir formu gerekiyor. Buna “Ayrık Zaman”, “Discrete Time” da dendiğini duyabilirsiniz.
$$\mathscr{F(\omega)} = \sum_{n= -\infty}^{n=\infty}x(n)e^{-j\omega n}$$
Sonlu toplam problemi çözdü sanırım, harika! Fakat negatif sonsuz ifadesi bizim için geçersiz.
$$\mathscr{F(\omega)} = \sum_{n= 0}^{n=\infty}x(n)e^{-j\omega n}$$
Burada üst limiti istediğiniz kadar arttırıp dönüşümü yapabilirsiniz fakat hala istediğimize tam ulaşamadık. Bilgisayar bilimi ile uğraşan arkadaşlar bilir ki algoritmaların bir çalışma süresi, performansı vardır. Bu yapı bilgisayarda uygulanmaya çalıştığından ciddi bir hız sorunu ortaya çıkar. Burada karşımıza optimize edilmiş bir algoritma olan “FFT” yani “Fast Fourier Transform” çıkar. FFT sadece bir algoritmadır, bir formül değildir! FFT oldukça hızlı çalışan bir algoritma olup bir çok donanımsal yapıya entegre edilebilir. Bu hız avantajı bilgisayarların yanı sıra MCU gibi küçük özellikteki donanımlara kadar entegre edilebilmesine olanak sağlar. Özellikle bilgisayar ortamında çalışıyorsanız Python bize büyük bir avantaj sağlıyor. Python’un büyük nimetlerinden olan Numpy, Scipy, MatPlot gibi kütüphaneler üzerinizden tonlarca yükü kaldırıyor. Aşağıda basit bir Python FFT örneği bulunuyor.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
from scipy.fftpack import fft import numpy as np import matplotlib.pyplot as plt N = 8192 f1 = 50 # 50 Hz f2 = 100 # 100 Hz A1 = 1/2 # 50 Hz A2 = 1/3 # 100 Hz T = 1.0 / 800.0 x = np.linspace(0.0, N*T, N) y = A1*np.sin(2.0*np.pi*f1*x) + A2*np.sin(2.0*np.pi*f2*x) yf = fft(y) xf = np.linspace(0.0, 1.0/(2.0*T), N//2) plt.plot(xf, 2.0/N * np.abs(yf[0:N//2])) plt.grid() plt.show() |
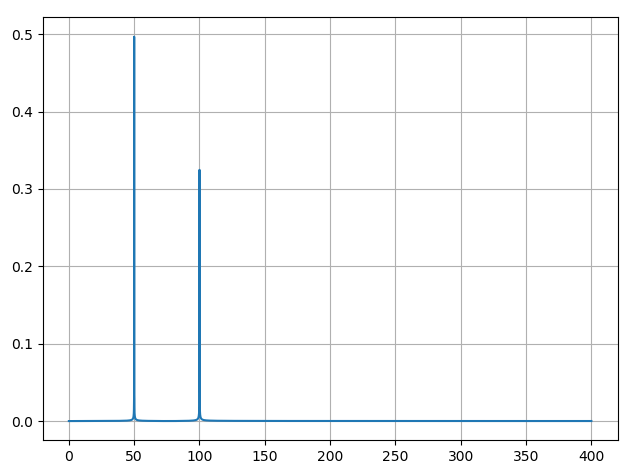
Bu kodu çalıştırdığınızda şu çıktıyı alırsınız.
Gördüğünüz gibi artık frekans düzlemini görebiliyor ve akabinde yorumlayabiliyoruz. Kısaca bütün şeytanları göz önüne çıkardık. İlerleyen yazılarda FFT işleminin daha küçük donanımlar olan MCU, FPGA gibi yapılarda uygulamasını yapacağız. Konuyu özet bir halde aktarıp basit bir örnekle pekiştirmek istedim. Şimdilik bu kadar.
Esen kalın.

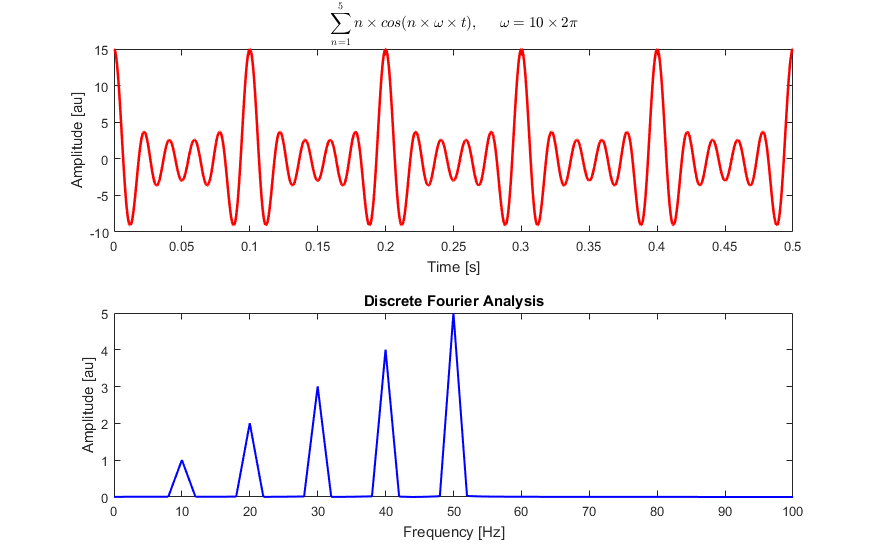

Baran teşekkürler basit anlatımın çok güzel. Her iki grafiğin birlikte çizildiği birinci şekle ilişkin python programını bana da gönderebilirmisin.
Selamlar İsmail Kaya