Fubini’s Theorem for Gauss Integral
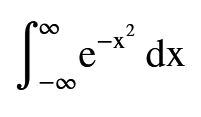 Calculus çalışırken “hadi bu soruyu birde bu hali ile çözeyim” derken çok garip gözüken bir integral yapısı ile karşılaştım.Değişken dönüşümü, Trigonometrik Yerine Koyma Metodu, Kesirlere ayırma, Kısmi integrasyon gibi yöntemlerle bu integrali çözmenin mümkün olmadığını fark edince aslında bu yapının “Gauss İntegrali” olarak geçtiğini gördüm.
Calculus çalışırken “hadi bu soruyu birde bu hali ile çözeyim” derken çok garip gözüken bir integral yapısı ile karşılaştım.Değişken dönüşümü, Trigonometrik Yerine Koyma Metodu, Kesirlere ayırma, Kısmi integrasyon gibi yöntemlerle bu integrali çözmenin mümkün olmadığını fark edince aslında bu yapının “Gauss İntegrali” olarak geçtiğini gördüm.
Çözümü için buna R diyip her iki tarafında karesini alarak çözüme başlayalım.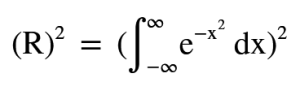 Sağ tarafı şöyle yazabiliriz.Burada 2.kısıma x değilde y olarak alalım.İkinci değişeni y almak sonuçları aynı olduğundan bir değişiklik oluşturmayacaktır.
Sağ tarafı şöyle yazabiliriz.Burada 2.kısıma x değilde y olarak alalım.İkinci değişeni y almak sonuçları aynı olduğundan bir değişiklik oluşturmayacaktır.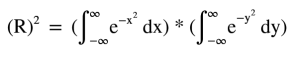 Çarpma durumunda olan bu 2 integrali iç içe yazabiliriz.Dışarıdaki integralin çözümü içerideki integrale kat sayı olarak gelecek.Katsayıdan kastım farklı bir değişken olduğu için içerideki integral çözülürken sabit bir sayı gibi kullanılacak.Gerçi iç kısım çözülürken değişken gelmeyecek direk sabit bir sayı geliyor.Bunu birazdan göreceğiz.Şimdi e üzerini eksi parantezine alalım.
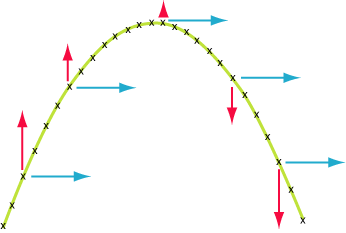
Çarpma durumunda olan bu 2 integrali iç içe yazabiliriz.Dışarıdaki integralin çözümü içerideki integrale kat sayı olarak gelecek.Katsayıdan kastım farklı bir değişken olduğu için içerideki integral çözülürken sabit bir sayı gibi kullanılacak.Gerçi iç kısım çözülürken değişken gelmeyecek direk sabit bir sayı geliyor.Bunu birazdan göreceğiz.Şimdi e üzerini eksi parantezine alalım.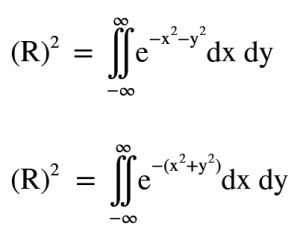 Şimdi bizim sorumuzda e üssüne dikkat ettiyseniz r’nin karesine olduğunu görmüşsünüzdür.Tabi bu dönüşümü yaptığımızda Kartezyen koordinat sisteminden Polar koordinat sistemine geçmiş oluyoruz.Bu yüzden dx ve dy diferansiyellerini de dönüştürmemiz gerekiyor.Önce polar sisteme geçtiğimizde bu ifadelerin nasıl bir hal aldığını görelim. Polar sistemde integral aldığımızda bu küçük dilimlerin nasıl olduğunu aşağıdaki şekilde görmekteyiz;
Şimdi bizim sorumuzda e üssüne dikkat ettiyseniz r’nin karesine olduğunu görmüşsünüzdür.Tabi bu dönüşümü yaptığımızda Kartezyen koordinat sisteminden Polar koordinat sistemine geçmiş oluyoruz.Bu yüzden dx ve dy diferansiyellerini de dönüştürmemiz gerekiyor.Önce polar sisteme geçtiğimizde bu ifadelerin nasıl bir hal aldığını görelim. Polar sistemde integral aldığımızda bu küçük dilimlerin nasıl olduğunu aşağıdaki şekilde görmekteyiz;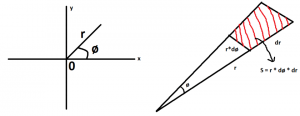
Ve artık biliyoruz ki 2 katlı integralde dx dy polar sisteme r dø dr olarak geçiyor.Peki sınırlar nasıl değişecek ? Öncelikle dr için konuşursak r nin değişim sınırları orjinden(0) sonsuza kadar olacaktır.Açı olan dø ise 0 dan 2π(360°) ye kadar olacaktır.Ufak bir görsel ile özetleyelim.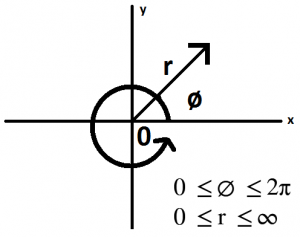 Ve artık integralin son halini yazıp çözelim.Tabi bu ifadenin R² olduğunu unutmayalım.
Ve artık integralin son halini yazıp çözelim.Tabi bu ifadenin R² olduğunu unutmayalım.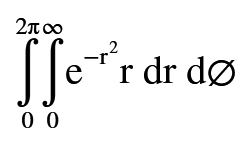 Bu kısımda Fubini’nin 1.Theorem’inden faydalanacağız.
Bu kısımda Fubini’nin 1.Theorem’inden faydalanacağız.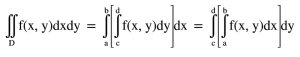
Bu Theorem den anlayacağımız üzere 2 katlı integrallerin ardışık olarak tek katlı integraller halinde çözebiliriz.İçerideki integrali çözersek sonsuz yerine b yazıp limit durumuna bakarak ilk integralin çözümünü tamamlayabiliriz.Sınırları sonsuz olan integralde limit ile çözmeyi de aşağıda adım adım gösterdim.Burada sadece basit bir değişken dönüşümü yaptım.Bildiğimiz “U” metodu.Değişken dönüşümünde sınırlarında değiştiğini unutmamalıyız.Çünkü U metodu uygularsak sınırlar 0 dan sonsuz yerine 0 dan -sonsuz’a gidecektir.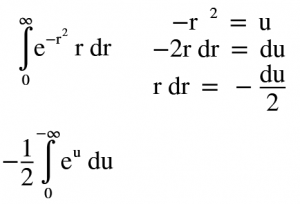 Bu basit hale indirgenmiş integralide kolayca çözüp limit ile sonsuz sınırınında çözümünü yaparak ilk integrali bitirelim.
Bu basit hale indirgenmiş integralide kolayca çözüp limit ile sonsuz sınırınında çözümünü yaparak ilk integrali bitirelim.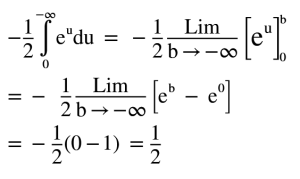
Ve böylece iç kısım tamamlanmış oluyor.Bu değeri dış kısımdaki integrale yazarak çözümü bitirelim.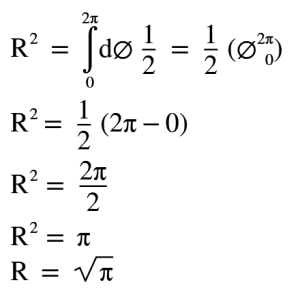
Gördüğümüz üzere R² nin π olduğuna ve R ninde √π ye eşit olduğunu gördük.Şimdi bu korkunç gözüken integraller aslında ne kadar rahat bir çözümü olduğunu öğrendik.Sanırım şimdilik bu kadar.Bir sonraki problemde görüşmek üzere.
Esen Kalın!

Son yorumlar