Trigonometric Substitutions

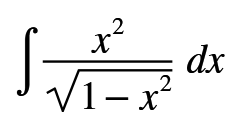Bugün yine İntegral çözüm metotlarından olan Trig Substitutions(Trigonometrik Yerine Koyma Metodu) ile karşılaştım.Fakat bu sefer ki biraz farklı ve bol dönüşümlü bir soru.Sözü fazla uzatmadan çözümü soru üzerinde anlatmak istiyorum.Bir yandan da yeni keşfettiğim Math Editor programında tanıtayım.

Bu tarz köklü ifadelerde yapılması gereken ilk adım bu integralin hangi tipte olduğunu bulmak.Köklü ifadelerde şu dönüşüm yapılabiliyor.

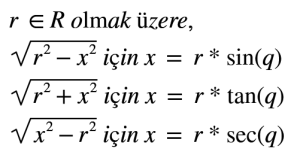
Bu dönüşümü yaptıktan sonra integrali çözüp q yerine Ters Trigonometrik fonksiyonu yerine yazıyoruz.Bizim örneğimiz de ilk dönüşümü kullanacağız bu durumda q yerine Arcsin(x) yazacağız.Şimdi x = r * sin(q) yazarsak r = 1 olduğundan x = sin(q) olur.Burada q lu bir ifade geldi fakat bizim integralimiz x’e göre çözülecek bu yüzden dx’i de buradan çekmek zorundayız.Her iki tarafında diferansiyelini alarak dx diferansiyelini buluyoruz.

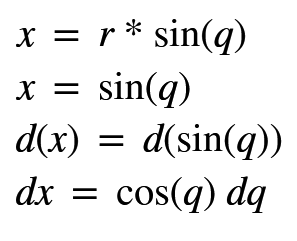
Şimdi yerine yazarak toparlayalım.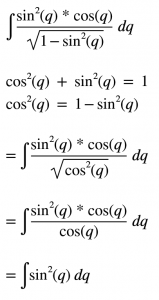

Ben burada alt kısımdaki işlemi sadeleştirdim.Şuan elimizde sin²(q) integralini almak kaldı. Bunun için yine trigonometrinin nimeti olan bir dönüşümden faydalanacağız.Buyursunlar…

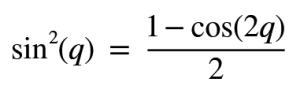
Yerine yazıp düzenleyelim.Bu adımlarda integrali yerine yazınca aradaki eksiden dolayı 2 ayrı integral olarak yazıp çözdüm.Ek olarak cos(2q) için ufak bir dönüşüm yaptık.

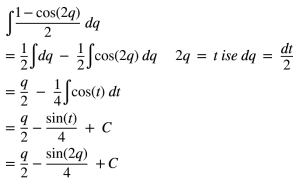
Şimdi en başta yaptığımız dönüşüme göre x = r * sin(q) ise sin(q) = x / r dir.Yan sin(q) = x olacaktır.Burada q yerine Arcsin(x) yazmalıyız.

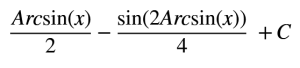
Normalde soru burada bitiyor.Ama o sol tarafı armut gibi bırakmak olmaz.Madem bu kadar geldik son bir dönüşüm daha yapacağız.Biliyor dönüşüm yapmaktan başınız döndü. Son olarak Arcsin(x) = y dersek şu sonucu elde ederiz.

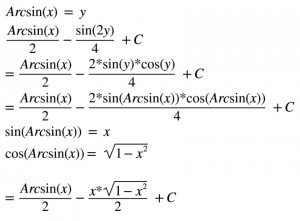
Ve işte sonuç Matlab ile kontrol ettim.Hatta onuda paylaşayım.

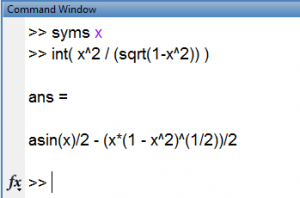
Bu güzel bol dönüşümlü soruyu çözdüğüm iyi oldu.Ters trigonometrik fonksiyonlarda yeni bilgiler edindim ve böylece Trig Sub Metodunuda az çok görmüş olduk.Şimdilik bu kadar.

Esen kalın!